Abstract: 44 words
Main Text: 1054 words
References: 277 words
Total Text: 1375 words
If a tree falls in the forest and there is nobody around, does Chasles' theorem still apply?
See a version with the movies for Figure 1.
Marco BertaminiBertamini, M. (2001). If a tree falls in the forest and there is nobody around, does Chasles' theorem still apply?, Behavioral and Brain Sciences, 24, 4, 655-656. Commentary on Todorovic, D. (2001) Is kinematic geometry an internalized regularity?
marco.bertamini@gmail.comhttp://www.bertamini.org/lab
Abstract
The limitations of the concept of internalised kinematic geometry have been recognised by Barlow, Hecht, Kubovy and Epstein, and Todorovic.
I am in agreement but I still find the perception of curvature in two frames apparent motion fascinating and I suggest some new directions.
Barlow, Hecht, Kubovy and Epstein, and Todorovic all argue against internalisation of kinematic geometry. I have argued along these lines in the past (Bertamini, 1996; Bertamini & Smit, 1998), in particular I share Todorovic's opinion that there is a fundamental difference between internalisation of physics and internalisation of mathematics (i.e., kinematic geometry). A succinct way of summarising the issue is the following: all theories of perceptual phenomena can be cast in mathematical terms, when we need to choose between them the differences, apart from their predictive power, can only be in their elegance or in their simplicity. Elegance brings the observer back into the equation and is therefore incompatible with internalisation, and simplicity is a principle closely related to Occam's rasor. The only possible evidence for internalisation of geometry is therefore simplicity. But as Todorovic shows, it is not always possible to establish which solution is simpler, because it depends on how the problem is formalised.
I also have more apparent motion data to contribute. Following the work of Proffitt et al. (1988) and using the window technique (McBeath & Shepard, 1989) we investigated systematically the effect of alpha. Figure 1a shows two frames (the first is the one on the left), alpha is -8deg, and the grey circle shows the rigid rotation. We found that perceived curvature increases monotonically as alpha goes from -45 to 45 (Bertamini & Smit, 1998). Note that changes in alpha do not change the center of rotation, and this effect is therefore inconsistent with the idea of internalised kinematic geometry. It suggests instead that motion tends to be orthogonal to the orientation of the object in the first frame.
Some observations on symmetric shapes are also important. Using a solid rectangle (Figure 1b) there are not only the two possible paths that are always possible on the basis of Chasles theorem (90 and 270deg respectively). There are two more paths identical to the first two except that alpha differs by 90deg. Ignoring the longer paths, we still have a conflict between two possible solutions with the same angle of rotation. Both solutions can be seen, but the motion orthogonal to the orientation of the object (alpha=0) is seen more often by naive subjects. In this solution the object extends farther from the center of rotation, therefore we may be observing a difference in torque. If so, this would be an effect related to the physics of the event, not its kinematic geometry.
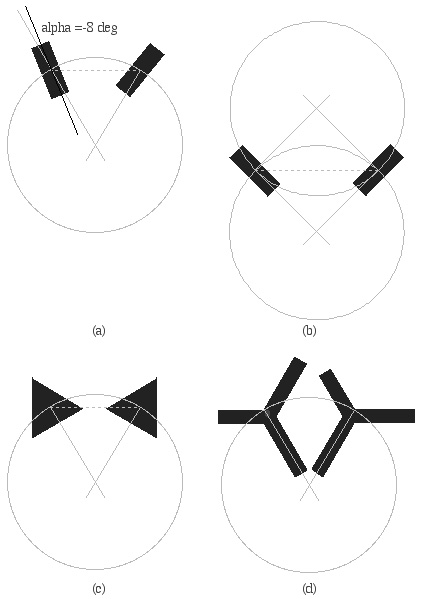
Figure 1. Animations can be seen at http://www.bertamini.org/lab/todorovic.html
More axes of symmetry can be present in an object, such as in the case of an equilateral triangle (Figure 1c). Kolers and Pomerantz (1971) have noticed that both rotation in the plane and rotation in depth can be seen in such cases (the depth solution being more likely with longer presentation time). What is important here is that a depth rotation of 180deg is seen at least as often as a rotation in the plane of 60deg. Surely this is a problem for an argument based on the simplicity of motion. We went even farther and tried quasi-symmetrical stimuli (Figure 1d). Remarkably, motion in depth is seen even when the 60deg rotation is a rigid motion whereas a rotation in depth of 180deg entails a shape change (one arm getting longer as the object moves).
Shepard discusses the case where motion in depth by 180deg is preferred to rotation by 180deg and suggests that the reason depth rotation is preferred is because it is more consistent with retinal stimulation (i.e., if motion in the plane had taken place it would have been detected). I doubt that this could account for the case where 180deg is compared to 60deg, but it is a useful way of looking at the problem (i.e., what is the most likely motion given the available evidence), especially if we agree that apparent motion is a solution to poor temporal sampling (Watson & Ahumada, 1983).
I hasten to acknowledge the noisiness of these data. Everybody looking at these displays will notice their inherent ambiguity. Percepts can and do change even for one individual over time. This multistability needs to be taken into account in any theoretical account. I suggest that this multistability could be used constructively to study the way shape is represented. Taking the example of the equilateral triangle, the three axes of bilateral symmetry are identical from a geometrical point of view, but perceptually they are not. At any one time, one vertex is seen as the top and the opposite side as the base of the object. Such chosen axis of orientation is important in determining the motion of the object (for other effects of shape on apparent motion see McBeath et al., 1992). When the equilateral triangle is seen as oriented horizontally, the motion in depth (but not the rotation in the plane) is around a pivot point along the axis of elongation. The importance of axes in constraining perceived motion is consistent with what Shepard has argued, except that I do not think this means that kinematic geometry has been internalised, it means that the representation of shape is not independent from the representation of motion.
We have recently found effects of pivot points in how motion is perceived using random dot configurations (Bertamini & Proffitt, 2000). These are all examples where the system assumes (or infers from spatial information) mechanical constraints on motion (Hoffman & Bennett, 1986). Given the environment in which we live, this may be the best strategy, the only case in which mechanical constraints to motion do not exist are particle motions and they are not as common as extended object motion and joint motion. Shepard claims that physics would predict straight paths for the center of mass, but although this is true it misses out on the fact that given a certain shape not all motions are equally likely. Probably no tree that has ever fallen in the forest moved along a straight path, instead it rotated around a center at the base of its elongation.
Finally, as an aside, I point out that the preference for motion orthogonal to object orientation is not a general effect. Werkhoven et al. (1990) have found the opposite result in short term apparent motion. This difference may be related to how the aperture problem affects the system at different scales. But this is another story.
References
Barlow, H. (2001). The Exploitation of Regularities in the Environment by the Brain.
Behavioral and Brain Sciences, 24 (3).
Bertamini M. (1996). The role of stimulus orientation in short- and long-range apparent motion.
ARVO meeting, Ft.Lauderdale, April 1996, IOVS 37, 3.
Bertamini M., Proffitt, D.R. (2000). Hierarchical motion organization in random dot configurations.
Journal of Experimental Psychology:
Human Perception and Performance, 26, 4, 1371-1386.
Bertamini M., Smit D.J.A. (1998). Minimization processes in apparent motion.
EMPG meeting, Sept 1998. Journal of Mathematical Psychology, 42, 4.
Hecht, H. (2001). Regularities of the Physical World and the Absence of their Internalization
Behavioral and Brain Sciences 24 (3).
Hoffman, D.D., & Bennett, B.M. (1986). The computation of structure from fixed-axis motion:
Rigid structures. Biological Cybernetics, 54, 71-83.
Kolers, P.A., & Pomerantz, J.R. (1971). Figural change in apparent motion.
Journal of Experimental Psychology, 87, 99-108.
Kubovy, M., & Epstein, W. (2001). Internalization: A metaphor we can live without.
Behavioral and Brain Sciences, 24 (3).
McBeath, M.K., Morikawa, K., & Kaiser,M. (1992). Perceptual bias for forward-facing motion.
Psychological Science, 3, 462-267.
McBeath, M.K.& Shepard R.N. (1989). Apparent Motion Between Shapes Differing in Location and Orientation: A Window Technique for Estimating Path Curvature. Perception & Psychophysics, 46, 333-337.
Proffitt, D.R., Gilden, D.L., Kaiser, M.K., & Whelan, S.M. (1988). The effect of configural orientation on perceived trajectory in apparent motion. Perception and Psychophysics, 43, 465-474.
Shepard, R. N. (1994). Perceptual-Cognitive Universals as Reflections of the World.
Psychonomic Bulletin & Review, 1, 2-28.
Todorovic, D. (2001). Is kinematic geometry an internalized regularity?
Behavioral and Brain Sciences, 24 (3).
Watson, A.B, & Ahumada, A.J. (1983). A look at motion in the frequency domain.
(Tech. Memo 84352). Washington D.C.: NASA.
Werkhoven, P., Snippe, P. & Koenderink, J. (1990).
Effects of element orientation on apparent motion perception.
Perception & Psychophysics, 47, 509-525.
